Proofs of the Sum, Difference, Product, and Quotient Rules
The Sum Rule
We begin with 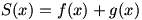 . We can write . We can write 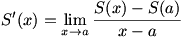 . The limit can be rewritten as . The limit can be rewritten as 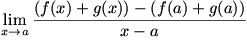 , or , or 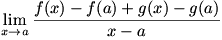 . The fraction can be split up into . The fraction can be split up into 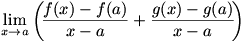 . We then apply the sum law to split the limit into . We then apply the sum law to split the limit into 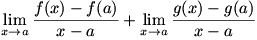 , which is simply , which is simply 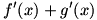 , so , so 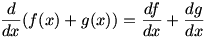 : the derivative of a sum is the sum of the derivatives. : the derivative of a sum is the sum of the derivatives.
The Difference Rule
In the last lesson we showed that 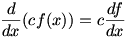 (this is a degenerate case of the Product Rule, proven below), so we can find (this is a degenerate case of the Product Rule, proven below), so we can find 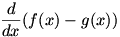 simply by regarding the second term as a constant of ‒1 times simply by regarding the second term as a constant of ‒1 times 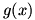 , so the difference rule is simply , so the difference rule is simply 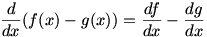 ; the derivative of a difference is the difference of the derivatives. ; the derivative of a difference is the difference of the derivatives.
The Product Rule
Working out 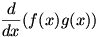 requires a bit of ingenuity. We begin the differentiation by writing the problem as a difference quotient: requires a bit of ingenuity. We begin the differentiation by writing the problem as a difference quotient: 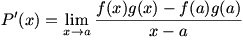 . Now, we play with the numerator, making the limit . Now, we play with the numerator, making the limit 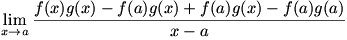 . This is valid, since we are both adding and subtracting the term . This is valid, since we are both adding and subtracting the term 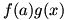 for a zero net change. We factor the numerator to give for a zero net change. We factor the numerator to give 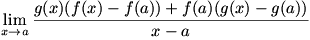 . Now we split the fraction and split the limit, just as we did to prove the sum rule; the expression left is . Now we split the fraction and split the limit, just as we did to prove the sum rule; the expression left is 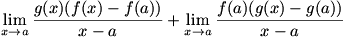 . We know that . We know that 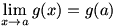 since since 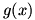 is continuous, and we can remove is continuous, and we can remove 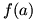 from the limit since it does not change as from the limit since it does not change as 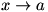 . Now we have . Now we have 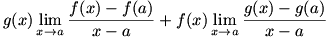 . The two limits each represent derivatives, so this expression is equal to . The two limits each represent derivatives, so this expression is equal to 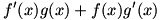 . Therefore the product rule states that . Therefore the product rule states that 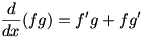 . (The constant multiple rule is a degenerate case of the product rule, since the derivative of a constant is zero.) . (The constant multiple rule is a degenerate case of the product rule, since the derivative of a constant is zero.)
The Quotient Rule
Given 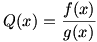 , we know that , we know that 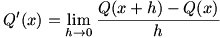 , a limit which can of course be written as , a limit which can of course be written as 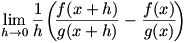 . We combine the two parts of the second term into one fraction, so we have . We combine the two parts of the second term into one fraction, so we have 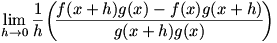 . Now we use a similar technique to that used in solving for the product rule: we add and subtract . Now we use a similar technique to that used in solving for the product rule: we add and subtract 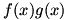 to and from the numerator. Now the limit is to and from the numerator. Now the limit is 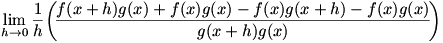 , which we factor to give , which we factor to give 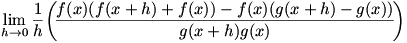 . Now we move the . Now we move the 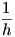 around a bit: around a bit: 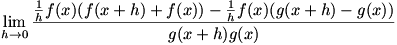 , which we rewrite as , which we rewrite as 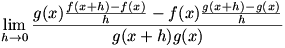 . It’s apparent now that there are some difference quotients in there, so we can make the limit into . It’s apparent now that there are some difference quotients in there, so we can make the limit into 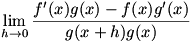 . And since . And since 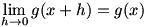 , we rewrite the denominator to give , we rewrite the denominator to give 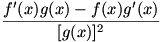 . .


| 